[ad_1]
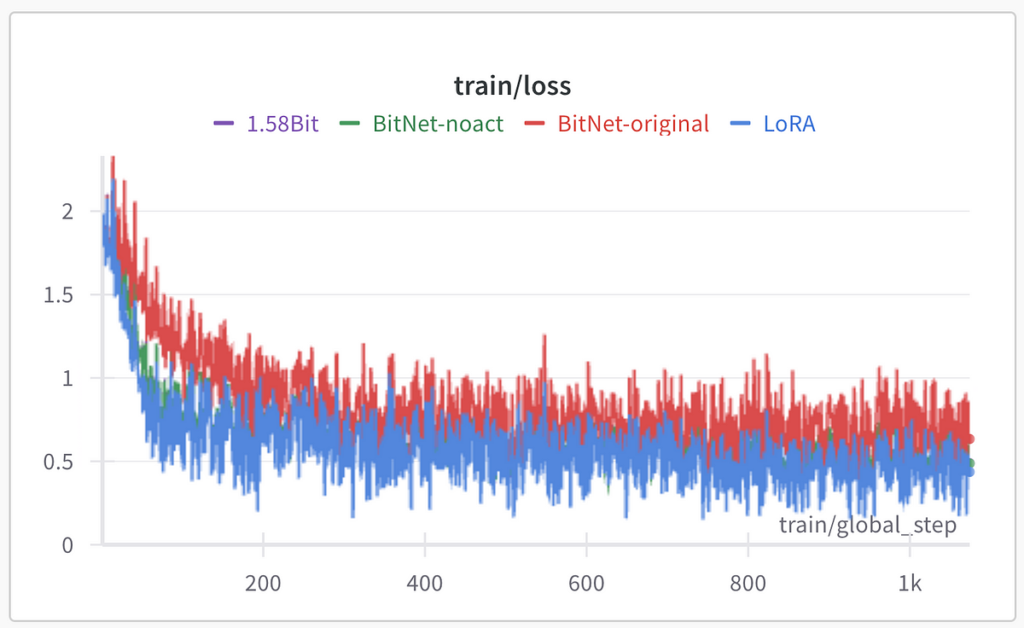
Đối với các thử nghiệm, tôi đã lấy dữ liệu độc quyền của mình cho nhiệm vụ tạo văn bản. Bản thân dữ liệu ở đây không quan trọng lắm, tôi chỉ nói rằng nó là một tập hợp con nhỏ của tập dữ liệu hướng dẫn được sử dụng để đào tạo hướng dẫn theo LLM. Là mô hình cơ bản, tôi quyết định sử dụng microsoft/Phi-3-mini-4k-hướng dẫn người mẫu. Tôi đã thực hiện 3 giai đoạn điều chỉnh bộ điều hợp LoRA với chương trình đào tạo có độ chính xác hỗn hợp fp16 bằng Huggingface Coach và đo lường mức độ tổn thất khi đánh giá. Sau đó, tôi đã triển khai BitNet (thay thế các lớp tuyến tính trong bộ điều hợp LoRA) và đào tạo LoRA 1,58 bit và báo cáo kết quả. Tôi đã sử dụng lượng tử hóa mô hình cơ sở 4 bit với BitsAndBytes trong quá trình đào tạo về cấu hình Q-LoRA.
Các siêu tham số LoRA sau đây đã được sử dụng: xếp hạng = 32, alpha = 16, tỷ lệ bỏ học = 0,05.
3.1. Đào tạo LoRA cổ điển
Đối với tất cả các thử nghiệm LoRA QLoRA Cách tiếp cận đã được sử dụng trong phần lượng tử hóa mô hình cơ sở với NF4 và áp dụng LoRA cho tất cả các lớp tuyến tính của mô hình cơ sở. Trình tối ưu hóa được phân trang AdamW với quá trình khởi động và ủ cosine xuống tới 90% tốc độ học tập tối đa. Tỷ lệ học tập tối đa bằng 2e-4. Việc phân chia đào tạo/kiểm tra là ngẫu nhiên, tập kiểm tra là 10% từ toàn bộ tập dữ liệu.
3.2. Triển khai LoRA BitNet
Đối với việc đào tạo BitNet LoRA, cách tiếp cận từ “BitNet: Chia tỷ lệ Máy biến áp 1 bit cho các mô hình ngôn ngữ lớn” đã được sử dụng với mã để thực hiện nó. Theo bài báo của BitNet, trọng số của các lớp LoRA đã được nhị phân hóa theo tỷ lệ:
Đồng thời kích hoạt cũng nên được lượng tử hóa theo bài báo:
Theo các công thức được cung cấp, bạn có thể thấy rằng mỗi tham số đang được biến đổi với hàm dấu là +1 hoặc -1, các tham số đó được nhân với đầu vào X được lượng tử hóa và chuẩn hóa và được chia tỷ lệ với giá trị tuyệt đối trung bình của các tham số của lớp. Triển khai mã:
from torch import nn, Tensor
import torch.nn.purposeful as F# from https://github.com/kyegomez/zeta
class SimpleRMSNorm(nn.Module):
"""
SimpleRMSNorm
Args:
dim (int): dimension of the embedding
Utilization:
We will use SimpleRMSNorm as a layer in a neural community as follows:
>>> x = torch.randn(1, 10, 512)
>>> simple_rms_norm = SimpleRMSNorm(dim=512)
>>> simple_rms_norm(x).form
torch.Measurement((1, 10, 512))
"""
def __init__(self, dim):
tremendous().__init__()
self.scale = dim**-0.5
def ahead(self, x):
"""Ahead methodology of SimpleRMSNorm"""
return F.normalize(x, dim=-1) * self.scale
def activation_quant(x: Tensor):
"""Per token quantization to 8bits. No grouping is required for quantization
Args:
x (Tensor): _description_
Returns:
_type_: _description_
"""
scale = 127.0 / x.abs().max(dim=-1, keepdim=True).values.clamp_(min=1e-5)
y = (x * scale).spherical().clamp_(-128, 127) / scale
return y
def weight_quant(w: Tensor):
scale = w.abs().imply()
e = w.imply()
u = (w - e).signal() * scale
return u
class BitLinear(nn.Linear):
"""
Customized linear layer with bit quantization.
Args:
dim (int): The enter dimension of the layer.
coaching (bool, elective): Whether or not the layer is in coaching mode or not. Defaults to False.
*args: Variable size argument record.
**kwargs: Arbitrary key phrase arguments.
Attributes:
dim (int): The enter dimension of the layer.
"""
def ahead(self, x: Tensor) -> Tensor:
"""
Ahead move of the BitLinear layer.
Args:
x (Tensor): The enter tensor.
Returns:
Tensor: The output tensor.
"""
w = self.weight
x_norm = SimpleRMSNorm(self.in_features)(x)
# STE utilizing detach
# the gradient of signal() or spherical() is usually zero
# so to coach the mannequin we have to do the next trick
# this trick results in "w" excessive precision weights replace
# whereas we're doing "pretend" quantisation through the ahead move
x_quant = x_norm + (activation_quant(x_norm) - x_norm).detach()
w_quant = w + (weight_quant(w) - w).detach()
y = F.linear(x_quant, w_quant)
return y
Tất cả các mã ở trên là từ https://github.com/kyegomez/BitNet Kho lưu trữ GitHub.
Sau khi huấn luyện LoRA, các trọng số của bộ điều hợp có thể được hợp nhất với mô hình cơ sở vì thực tế là mỗi bộ điều hợp LoRA chỉ là một cặp lớp tuyến tính không có độ lệch và kích hoạt phi tuyến tính. Việc chuẩn hóa các kích hoạt (LN(x)) và lượng tử hóa của chúng theo cách tiếp cận đang khiến việc hợp nhất các bộ điều hợp LoRA trở nên khó khăn hơn (sau khi hợp nhất, bộ điều hợp LoRA chia sẻ cùng một đầu vào cho lớp tuyến tính như mô hình cơ sở – các lớp này hoạt động với các kích hoạt mà không có bất kỳ sửa đổi bổ sung nào) , đó là lý do tại sao thử nghiệm bổ sung không chuẩn hóa và lượng tử hóa kích hoạt đã được tiến hành và dẫn đến hiệu suất tốt hơn. Để thực hiện những sửa đổi như vậy, chúng ta chỉ cần sửa đổi phương thức chuyển tiếp của lớp BitLinear:
def ahead(self, x: Tensor) -> Tensor:
"""
Ahead move of the BitLinear layer.Args:
x (Tensor): The enter tensor.
Returns:
Tensor: The output tensor.
"""
w = self.weight
#x_norm = SimpleRMSNorm(self.in_features)(x)
# STE utilizing detach
#x_quant = x_norm + (activation_quant(x_norm) - x_norm).detach()
x_quant = x
w_quant = w + (weight_quant(w) - w).detach()
y = F.linear(x_quant, w_quant)
return y
Mã được trình bày là quá trình đào tạo nhận biết lượng tử hóa, bởi vì trọng số chính của mỗi lớp BitLinear vẫn có độ chính xác cao, trong khi chúng tôi nhị phân hóa các trọng số trong quá trình chuyển tiếp (điều tương tự chúng tôi có thể làm trong quá trình suy luận mô hình). Vấn đề duy nhất ở đây là chúng tôi còn có một tham số “tỷ lệ” riêng cho từng lớp và có độ chính xác cao.
Sau khi nhận được các lớp BitLinear, chúng ta cần thay thế các lớp tuyến tính trong bộ điều hợp LoRA bằng các lớp tuyến tính mới này để áp dụng sửa đổi BitLinear cho LoRA cổ điển. Để làm như vậy, chúng ta có thể viết lại phương thức “update_layer” của lớp LoraLayer (peft.tuners.lora.layer.LoraLayer) bằng cùng một phương thức nhưng với các lớp BitLinear thay vì Linear:
from peft.tuners.lora.layer import LoraLayer
import torch
import torch.nn.purposeful as F
from torch import nnclass BitLoraLayer(LoraLayer):
def update_layer(
self, adapter_name, r, lora_alpha, lora_dropout, init_lora_weights, use_rslora, use_dora: bool = False
):
if r <= 0:
increase ValueError(f"`r` needs to be a optimistic integer worth however the worth handed is {r}")
self.r(adapter_name) = r
self.lora_alpha(adapter_name) = lora_alpha
if lora_dropout > 0.0:
lora_dropout_layer = nn.Dropout(p=lora_dropout)
else:
lora_dropout_layer = nn.Identification()
self.lora_dropout.replace(nn.ModuleDict({adapter_name: lora_dropout_layer}))
# Precise trainable parameters
# The one replace of the unique methodology is right here
self.lora_A(adapter_name) = BitLinear(self.in_features, r, bias=False)
self.lora_B(adapter_name) = BitLinear(r, self.out_features, bias=False)
if use_rslora:
self.scaling(adapter_name) = lora_alpha / math.sqrt(r)
else:
self.scaling(adapter_name) = lora_alpha / r
if isinstance(init_lora_weights, str) and init_lora_weights.startswith("pissa"):
self.pissa_init(adapter_name, init_lora_weights)
elif init_lora_weights == "loftq":
self.loftq_init(adapter_name)
elif init_lora_weights:
self.reset_lora_parameters(adapter_name, init_lora_weights)
# verify weight and qweight (for GPTQ)
for weight_name in ("weight", "qweight"):
weight = getattr(self.get_base_layer(), weight_name, None)
if weight is just not None:
# the layer is already utterly initialized, that is an replace
if weight.dtype.is_floating_point or weight.dtype.is_complex:
self.to(weight.machine, dtype=weight.dtype)
else:
self.to(weight.machine)
break
if use_dora:
self.dora_init(adapter_name)
self.use_dora(adapter_name) = True
else:
self.use_dora(adapter_name) = False
self.set_adapter(self.active_adapters)
Sau khi tạo một lớp như vậy, chúng ta có thể thay thế phương thức update_layer của LoraLayer ban đầu bằng lớp mới:
import importlibunique = importlib.import_module("peft")
unique.tuners.lora.layer.LoraLayer.update_layer = (
BitLoraLayer.update_layer
)
3.3. LoRA 1,58 bit
Đối với thí nghiệm này, cách tiếp cận từ “Kỷ nguyên của LLM 1 bit: Tất cả các mô hình ngôn ngữ lớn đều ở dạng 1,58 bit” đã được dùng. Sự khác biệt về mặt khái niệm là thay vì nhị phân hóa thành +1 và -1 trong bài báo này, các tác giả đề xuất lượng tử hóa các trọng số thành -1, 0 và +1 để có độ chính xác cao hơn.
Các tác giả đã loại trừ các kích hoạt mở rộng quy mô khỏi quy trình đang tạo thêm khó khăn cho việc hợp nhất với mô hình cơ sở trong các thử nghiệm của chúng tôi. Trong các thử nghiệm của mình, chúng tôi cũng đã loại bỏ lượng tử hóa kích hoạt khỏi quy trình để giúp việc hợp nhất bộ điều hợp LoRA trở nên đơn giản hơn.
Để điều chỉnh bộ điều hợp LoRA theo phương pháp này, chúng ta chỉ cần cập nhật hàm Weight_quant bằng cách sau:
def weight_quant(w: Tensor):
scale = w.abs().imply()
adjustment = 1e-4 + scale / 2
w_quant = w / adjustment
return torch.clip(enter=torch.spherical(w_quant), min=-1, max=1)*scale
Để triển khai 1,58 bit tôi đã sử dụng Ấn bản “Phép thuật nhị phân: Xây dựng BitNet 1.58bit bằng PyTorch từ đầu” như điểm khởi đầu.
[ad_2]
Source link