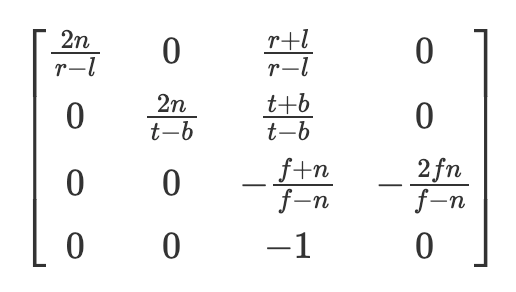Giới thiệu của Kỹ sư Python về Tách Gaussian 3D (Phần 2) | của Derek Austin | Tháng 6 năm 2024

Hiểu và mã hóa cách sử dụng Gaussian trong Phân chia Gaussian 3D

Bây giờ chuyển sang gaussian! Phân phối yêu thích của mọi người. Nếu bạn mới tham gia cùng chúng tôi, chúng tôi đã đề cập đến cách lấy điểm 3D và dịch nó sang 2D dựa trên vị trí của máy ảnh trong phần 1. Đối với bài viết này, chúng ta sẽ chuyển sang xử lý phần gaussian của quá trình phân chia gaussian. Chúng tôi sẽ sử dụng part_2.ipynb trong GitHub.

Một thay đổi nhỏ mà chúng tôi sẽ thực hiện ở đây là chúng tôi sẽ sử dụng phép chiếu phối cảnh sử dụng ma trận bên trong khác với ma trận được hiển thị trong bài viết trước. Tuy nhiên, cả hai đều tương đương nhau khi chiếu một điểm lên 2D và tôi thấy phương pháp đầu tiên được giới thiệu trong phần 1 dễ hiểu hơn nhiều, tuy nhiên, chúng tôi thay đổi phương pháp của mình để sao chép, bằng python, càng nhiều mã của tác giả càng tốt. Cụ thể, ma trận “nội bộ” của chúng ta bây giờ sẽ được đưa ra bởi ma trận chiếu OpenGL được hiển thị ở đây và thứ tự nhân bây giờ sẽ là [email protected]() @ nội bộ.

Đối với những người tò mò muốn biết về ma trận bên trong mới này (nếu không, vui lòng bỏ qua đoạn này) r và l là các mặt phẳng cắt của bên phải và bên trái, về cơ bản những điểm có thể được xem liên quan đến chiều rộng của ảnh và t và b là các mặt phẳng cắt trên và dưới. N là mặt phẳng cắt gần (nơi các điểm sẽ được chiếu tới) và f là mặt phẳng cắt xa. Để biết thêm thông tin, tôi thấy các chương của Scratchapixel ở đây khá nhiều thông tin (https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/opengl-perspective-projection-matrix.html). Điều này cũng trả về các điểm trong tọa độ thiết bị được chuẩn hóa (trong khoảng từ -1 đến 1) và sau đó chúng tôi chiếu tới tọa độ pixel. Lạc đề sang một bên, nhiệm vụ vẫn giữ nguyên, lấy điểm ở dạng 3D và chiếu lên mặt phẳng hình ảnh 2D. Tuy nhiên, trong phần hướng dẫn này, chúng ta hiện đang sử dụng gaussian thay vì điểm.

def getIntinsicMatrix(
focal_x: torch.Tensor,
focal_y: torch.Tensor,
top: torch.Tensor,
width: torch.Tensor,
znear: torch.Tensor = torch.Tensor((100.0)),
zfar: torch.Tensor = torch.Tensor((0.001)),,
) -> torch.Tensor:
"""
Will get the inner perspective projection matrix
znear: close to airplane set by person
zfar: far airplane set by person
fovX: area of view in x, calculated from the focal size
fovY: area of view in y, calculated from the focal size
"""
fovX = torch.Tensor((2 * math.atan(width / (2 * focal_x))))
fovY = torch.Tensor((2 * math.atan(top / (2 * focal_y))))
tanHalfFovY = math.tan((fovY / 2))
tanHalfFovX = math.tan((fovX / 2))
high = tanHalfFovY * znear
backside = -top
proper = tanHalfFovX * znear
left = -right
P = torch.zeros(4, 4)
z_sign = 1.0
P(0, 0) = 2.0 * znear / (proper - left)
P(1, 1) = 2.0 * znear / (high - backside)
P(0, 2) = (proper + left) / (proper - left)
P(1, 2) = (high + backside) / (high - backside)
P(3, 2) = z_sign
P(2, 2) = z_sign * zfar / (zfar - znear)
P(2, 3) = -(zfar * znear) / (zfar - znear)
return P

Biểu đồ gaussian 3D bao gồm tọa độ x, y và z cũng như ma trận hiệp phương sai liên quan. Như các tác giả đã lưu ý: “Một cách tiếp cận rõ ràng là tối ưu hóa trực tiếp ma trận hiệp phương sai Σ để thu được các gaussian 3D đại diện cho trường bức xạ. Tuy nhiên, ma trận hiệp phương sai chỉ có ý nghĩa vật lý khi chúng nửa xác định dương. Để tối ưu hóa tất cả các tham số của mình, chúng tôi sử dụng phương pháp giảm độ dốc không thể dễ dàng bị hạn chế để tạo ra các ma trận hợp lệ như vậy, đồng thời các bước cập nhật và độ dốc có thể rất dễ dàng tạo ra các ma trận hiệp phương sai không hợp lệ.”¹

Do đó, các tác giả sử dụng cách phân rã ma trận hiệp phương sai sẽ luôn tạo ra các ma trận hiệp phương sai bán xác định dương. Cụ thể, họ sử dụng 3 tham số “tỷ lệ” và 4 quaternion được chuyển thành ma trận xoay 3×3 (R). Ma trận hiệp phương sai sau đó được đưa ra bởi

Lưu ý người ta phải chuẩn hóa vectơ quaternion trước khi chuyển đổi sang ma trận xoay để có được ma trận xoay hợp lệ. Do đó, trong quá trình triển khai của chúng tôi, điểm gaussian bao gồm các tham số, tọa độ (vectơ 3×1), quaternions (vectơ 4×1), tỷ lệ (vectơ 3×1) và giá trị float cuối cùng liên quan đến độ mờ (mức độ trong suốt của biểu tượng) sau đây. Bây giờ tất cả những gì chúng ta cần làm là tối ưu hóa 11 thông số này để có được cảnh của mình – đơn giản đúng không!

Chà, hóa ra nó phức tạp hơn thế một chút. Nếu bạn nhớ lại môn toán trung học, độ mạnh của gaussian tại một điểm cụ thể được tính theo phương trình:

Tuy nhiên, chúng tôi quan tâm đến sức mạnh của gaussian 3D trong 2D, tức là. trong mặt phẳng ảnh. Nhưng bạn có thể nói, chúng tôi biết cách chiếu điểm lên 2D! Mặc dù vậy, chúng tôi vẫn chưa tiến hành chiếu ma trận hiệp phương sai thành 2D và vì vậy chúng tôi không thể tìm thấy nghịch đảo của ma trận hiệp phương sai 2D nếu chúng tôi chưa tìm thấy ma trận hiệp phương sai 2D.

Bây giờ mới là phần thú vị (tùy thuộc vào cách bạn nhìn nhận nó). EWA Splatting, một tài liệu tham khảo trên giấy của các tác giả phân tách gaussian 3D, chỉ ra chính xác cách chiếu ma trận hiệp phương sai 3D thành 2D.² Tuy nhiên, điều này đòi hỏi kiến ​​thức về ma trận biến đổi affine Jacobian mà chúng tôi tính toán bên dưới. Tôi thấy mã hữu ích nhất khi xem qua một khái niệm khó và do đó tôi đã cung cấp một số mã bên dưới để minh họa cách chuyển từ ma trận hiệp phương sai 3D sang 2D.

def compute_2d_covariance(
factors: torch.Tensor,
external_matrix: torch.Tensor,
covariance_3d: torch.Tensor,
tan_fovY: torch.Tensor,
tan_fovX: torch.Tensor,
focal_x: torch.Tensor,
focal_y: torch.Tensor,
) -> torch.Tensor:
"""
Compute the 2D covariance matrix for every gaussian
"""
factors = torch.cat(
(factors, torch.ones(factors.form(0), 1, gadget=factors.gadget)), dim=1
)
points_transformed = (factors @ external_matrix)(:, :3)
limx = 1.3 * tan_fovX
limy = 1.3 * tan_fovY
x = points_transformed(:, 0) / points_transformed(:, 2)
y = points_transformed(:, 1) / points_transformed(:, 2)
z = points_transformed(:, 2)
x = torch.clamp(x, -limx, limx) * z
y = torch.clamp(y, -limy, limy) * z
J = torch.zeros((points_transformed.form(0), 3, 3), gadget=covariance_3d.gadget)
J(:, 0, 0) = focal_x / z
J(:, 0, 2) = -(focal_x * x) / (z**2)
J(:, 1, 1) = focal_y / z
J(:, 1, 2) = -(focal_y * y) / (z**2)
# transpose as initially arrange for perspective projection
# so we now rework again
W = external_matrix(:3, :3).T
return (J @ W @ covariance_3d @ W.T @ J.transpose(1, 2))(:, :2, :2)

Trước hết, tan_fovY và tan_fovX là các tiếp tuyến của một nửa trường góc nhìn. Chúng tôi sử dụng các giá trị này để hạn chế các phép chiếu của mình, ngăn chặn mọi phép chiếu ngoài màn hình hoang dã ảnh hưởng đến kết xuất của chúng tôi. Người ta có thể rút ra jacobian từ phép biến đổi từ 3D sang 2D như đã cho với phép biến đổi thuận ban đầu được giới thiệu trong phần 1, nhưng tôi đã giúp bạn tránh khỏi rắc rối và hiển thị đạo hàm mong đợi ở trên. Cuối cùng, nếu bạn còn nhớ, chúng tôi đã chuyển đổi ma trận xoay ở trên để phù hợp với việc sắp xếp lại các số hạng và do đó chúng tôi chuyển đổi trở lại dòng áp chót trước khi trả về phép tính hiệp phương sai cuối cùng. Như giấy ghi chú của EWA, chúng ta có thể bỏ qua hàng và cột thứ ba vì chúng ta chỉ quan tâm đến mặt phẳng hình ảnh 2D. Bạn có thể thắc mắc, tại sao chúng ta không thể làm điều đó ngay từ đầu? Chà, các tham số ma trận hiệp phương sai sẽ thay đổi tùy thuộc vào góc độ bạn đang xem nó vì trong hầu hết các trường hợp, nó sẽ không phải là một hình cầu hoàn hảo! Bây giờ chúng ta đã chuyển đổi sang quan điểm chính xác, thông tin trục z hiệp phương sai là vô ích và có thể bị loại bỏ.

Cho rằng chúng ta có ma trận hiệp phương sai 2D, chúng ta gần có thể tính toán tác động của mỗi gaussian lên bất kỳ pixel ngẫu nhiên nào trong hình ảnh của chúng ta, chúng ta chỉ cần tìm ma trận hiệp phương sai đảo ngược. Hãy nhớ lại trong đại số tuyến tính rằng để tìm nghịch đảo của ma trận 2×2, bạn chỉ cần tìm định thức và sau đó thực hiện một số thao tác xáo trộn các số hạng. Đây cũng là một số mã để giúp hướng dẫn bạn thực hiện quá trình đó.

def compute_inverted_covariance(covariance_2d: torch.Tensor) -> torch.Tensor:
"""
Compute the inverse covariance matrix
For a 2x2 matrix
given as
((a, b),
(c, d))
the determinant is advert - bc
To get the inverse matrix reshuffle the phrases like so
and multiply by 1/determinant
((d, -b),
(-c, a)) * (1 / determinant)
"""
determinant = (
covariance_2d(:, 0, 0) * covariance_2d(:, 1, 1)
- covariance_2d(:, 0, 1) * covariance_2d(:, 1, 0)
)
determinant = torch.clamp(determinant, min=1e-3)
inverse_covariance = torch.zeros_like(covariance_2d)
inverse_covariance(:, 0, 0) = covariance_2d(:, 1, 1) / determinant
inverse_covariance(:, 1, 1) = covariance_2d(:, 0, 0) / determinant
inverse_covariance(:, 0, 1) = -covariance_2d(:, 0, 1) / determinant
inverse_covariance(:, 1, 0) = -covariance_2d(:, 1, 0) / determinant
return inverse_covariance

Và tada, giờ đây chúng ta có thể tính toán cường độ pixel cho từng pixel trong một hình ảnh. Tuy nhiên, làm như vậy là cực kỳ chậm và không cần thiết. Ví dụ: chúng ta thực sự không cần lãng phí sức mạnh tính toán để tìm ra cách một biểu tượng ở (0,0) ảnh hưởng đến một pixel ở (1000, 1000), trừ khi ma trận hiệp phương sai rất lớn. Do đó, các tác giả đưa ra lựa chọn để tính cái mà họ gọi là “bán kính” của mỗi biểu tượng. Như đã thấy trong đoạn mã bên dưới, chúng tôi tính toán các giá trị riêng dọc theo mỗi trục (hãy nhớ rằng các giá trị riêng hiển thị sự thay đổi). Sau đó, chúng tôi lấy căn bậc hai của giá trị riêng lớn nhất để có thước đo độ lệch chuẩn và nhân nó với 3,0, bao gồm 99,7% phân bố trong phạm vi 3 độ lệch chuẩn. Bán kính này giúp chúng ta tìm ra các giá trị x và y tối thiểu và tối đa mà biểu tượng chạm vào. Khi kết xuất, chúng tôi chỉ tính toán cường độ điểm ảnh cho các pixel trong các giới hạn này, giúp tiết kiệm rất nhiều phép tính không cần thiết. Khá thông minh phải không?

def compute_extent_and_radius(covariance_2d: torch.Tensor):
mid = 0.5 * (covariance_2d(:, 0, 0) + covariance_2d(:, 1, 1))
det = covariance_2d(:, 0, 0) * covariance_2d(:, 1, 1) - covariance_2d(:, 0, 1) ** 2
intermediate_matrix = (mid * mid - det).view(-1, 1)
intermediate_matrix = torch.cat(
(intermediate_matrix, torch.ones_like(intermediate_matrix) * 0.1), dim=1
)
max_values = torch.max(intermediate_matrix, dim=1).values
lambda1 = mid + torch.sqrt(max_values)
lambda2 = mid - torch.sqrt(max_values)
# now we've the eigenvalues, we will calculate the max radius
max_radius = torch.ceil(3.0 * torch.sqrt(torch.max(lambda1, lambda2)))
return max_radius

Tất cả các bước trên cung cấp cho chúng tôi cảnh được xử lý trước, sau đó có thể được sử dụng trong bước kết xuất. Tóm lại, giờ đây chúng ta có các điểm trong 2D, các màu được liên kết với các điểm đó, hiệp phương sai trong 2D, hiệp phương sai nghịch đảo trong 2D, thứ tự độ sâu được sắp xếp, các giá trị x tối thiểu, y tối thiểu, x tối đa, y tối đa cho mỗi biểu tượng và các giá trị liên quan độ mờ đục. Với tất cả các thành phần này, cuối cùng chúng ta cũng có thể chuyển sang hiển thị hình ảnh!