Tensor là gì?

Giới thiệu

Giả sử bạn đang tham gia vào một dự án đầy thử thách, như mô phỏng các hiện tượng trong thế giới thực hoặc phát triển một dự án tiên tiến mạng lưới nơ-ron để dự báo các kiểu thời tiết. Tensor là các thực thể toán học phức tạp hoạt động ẩn và cung cấp năng lượng cho các phép tính phức tạp này. Tensor xử lý dữ liệu đa chiều một cách hiệu quả, giúp các dự án sáng tạo như vậy trở nên khả thi. Bài viết này nhằm mục đích cung cấp cho độc giả hiểu biết toàn diện về tenxơ, các đặc tính và ứng dụng của tenxơ. Là một nhà nghiên cứu, chuyên gia hoặc sinh viên, việc hiểu biết vững chắc về tenxơ sẽ giúp bạn xử lý dữ liệu phức tạp và các mô hình máy tính tiên tiến.

Tổng quan

• Định nghĩa tenxơ là gì và hiểu các dạng và chiều khác nhau của nó.
• Nhận biết các tính chất và phép toán liên quan đến tenxơ.
• Áp dụng khái niệm tenxơ vào nhiều lĩnh vực khác nhau như vật lý và học máy.
• Thực hiện các phép toán và chuyển đổi tenxơ cơ bản bằng Python.
• Hiểu được các ứng dụng thực tế của tenxơ trong mạng nơ-ron.

Tensor là gì?

Về mặt toán học, tenxơ là các đối tượng mở rộng ma trận, vectơ và vô hướng lên các chiều cao hơn. Các lĩnh vực khoa học máy tính, kỹ thuật và vật lý đều phụ thuộc rất nhiều vào tenxơ, đặc biệt là khi nói đến học kĩ càng Và học máy.

Nói một cách đơn giản, tenxơ là một mảng các số có thể có chiều. Hạng của tenxơ là số chiều. Đây là lời giải thích:

• Vô hướng: Một số duy nhất (tenxơ hạng 0).
• Véc tơ: Mảng số một chiều (tenxơ hạng 1).
• Ma trận: Mảng số hai chiều (tenxơ bậc 2).
• Tenxơ bậc cao hơn: Mảng có ba chiều trở lên (hạng 3 trở lên).

Về mặt toán học, một tenxơ có thể được biểu diễn như sau:

• Một số vô hướng ( s ) có thể được biểu thị là ( s ).
• Một vectơ ( v ) có thể được biểu thị là ( v_i ) trong đó ( i ) là một chỉ số.
• Ma trận ( M ) có thể được biểu thị là ( M_{ij} ) trong đó ( i ) và ( j ) là các chỉ số.
• Một tenxơ bậc cao hơn ( T ) có thể được biểu thị là ( T_{ijk…} ) trong đó ( i, j, okay, ) v.v., là các chỉ số.

Tính chất của Tensor

Tensor có một số đặc tính khiến chúng trở thành công cụ đa năng và mạnh mẽ trong nhiều lĩnh vực:

• Kích thước: Số lượng chỉ số cần thiết để mô tả tenxơ.
• Thứ tự xếp hạng): Số chiều của một tenxơ.
• Hình dạng: Kích thước của mỗi chiều. Ví dụ, một tenxơ có hình dạng (3, 4, 5) có chiều là 3, 4 và 5.
• Kiểu:Tensor có thể lưu trữ nhiều loại dữ liệu khác nhau, chẳng hạn như số nguyên, số dấu phẩy động, v.v.

Tensor trong Toán học

Trong toán học, tenxơ khái quát các khái niệm như vô hướng, vectơ và ma trận thành các cấu trúc phức tạp hơn. Chúng rất cần thiết trong nhiều lĩnh vực, từ đại số tuyến tính đến hình học vi phân.

Ví dụ về số vô hướng và vectơ

• Vô hướng: Một số duy nhất. Ví dụ, nhiệt độ tại một điểm trong không gian có thể được biểu diễn dưới dạng giá trị vô hướng, chẳng hạn như (s = 37) độ C.
• Véc tơ: Một mảng số có độ lớn và hướng trong một chiều. Ví dụ, một vectơ (v = (3, 4, 5)) có thể được sử dụng để mô tả vận tốc của một vật thể chuyển động, trong đó mỗi phần tử biểu diễn thành phần vận tốc theo một hướng cụ thể.

Ví dụ về Tensor trong Đại số tuyến tính

Xét một ma trận ( M ), là một tenxơ hai chiều:

Dữ liệu đa chiều, chẳng hạn như hình ảnh có ba kênh màu, có thể được biểu diễn bằng tenxơ phức tạp như tenxơ bậc 3, trong khi ma trận được sử dụng cho các phép biến đổi như quay hoặc vectơ tỷ lệ trong một mặt phẳng. Kích thước liên quan đến độ sâu của màu, chiều rộng và chiều cao.

Ví dụ về sự co Tensor

Sự co lại của tenxơ là một sự tổng quát hóa của phép nhân ma trận. Ví dụ, nếu chúng ta có hai ma trận ( A ) và ( B ):

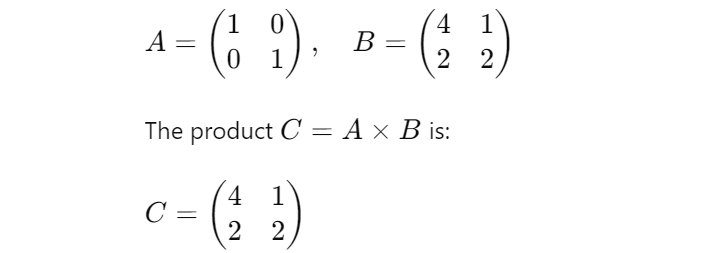
Tại đây, các chỉ số của ( A ) và ( B ) được cộng lại để tạo ra các phần tử của ( C ). Khái niệm này mở rộng sang các tenxơ bậc cao hơn, cho phép thực hiện các phép biến đổi và phép toán phức tạp trong không gian đa chiều.

Tensor trong Khoa học máy tính và Học máy

Tensor đóng vai trò quan trọng trong việc tổ chức và phân tích dữ liệu đa chiều trong khoa học máy tính và học máy, đặc biệt là trong các nền tảng học sâu như PyTorch và TensorFlow.

Sự miêu tả dữ liệu

Tensor được sử dụng để biểu diễn nhiều dạng dữ liệu khác nhau:

• Số vô hướng: Được biểu diễn dưới dạng tenxơ hạng 0. Ví dụ, một giá trị số duy nhất, chẳng hạn như tốc độ học trong thuật toán học máy.
• Các vectơ: Được biểu diễn dưới dạng tenxơ bậc 1. Ví dụ, danh sách các tính năng cho một điểm dữ liệu, chẳng hạn như cường độ điểm ảnh trong ảnh thang độ xám.
• Ma trận: Là biểu diễn tenxơ bậc 2, thường được sử dụng để lưu trữ các tập dữ liệu trong đó tính năng được biểu diễn bằng một cột và mẫu dữ liệu được biểu diễn bằng một hàng.
• Tensor bậc cao hơn: Được sử dụng với các định dạng dữ liệu phức tạp hơn. Ví dụ, một tenxơ bậc 3 có kích thước (chiều cao, chiều rộng, kênh) có thể được sử dụng để biểu diễn một hình ảnh màu.

Tensor trong Học sâu

Trong học sâu, tenxơ được sử dụng để biểu diễn:

• Dữ liệu đầu vào: Dữ liệu thô được đưa vào mạng nơ-ron. Ví dụ, một lô hình ảnh có thể được biểu diễn dưới dạng tenxơ 4 chiều có hình dạng (kích thước lô, chiều cao, chiều rộng, kênh).
• Trọng số và Độ lệch: Các tham số của mạng nơ-ron được học trong quá trình đào tạo. Chúng cũng được biểu diễn dưới dạng tenxơ có hình dạng thích hợp.
• Kích hoạt trung gian: Đầu ra của mỗi lớp trong mạng nơ-ron, cũng là các tenxơ.

Ví dụ

Hãy xem xét một mạng nơ-ron đơn giản với một lớp đầu vào, một lớp ẩn và một lớp đầu ra. Dữ liệu và tham số ở mỗi lớp được biểu diễn dưới dạng tenxơ:

import torch

# Enter knowledge: batch of two photos, every 3x3 pixels with 3 colour channels (RGB)
input_data = torch.tensor(((((1, 2, 3), (4, 5, 6), (7, 8, 9)),
                            ((9, 8, 7), (6, 5, 4), (3, 2, 1)),
                            ((0, 0, 0), (1, 1, 1), (2, 2, 2))),
                           (((2, 3, 4), (5, 6, 7), (8, 9, 0)),
                            ((0, 9, 8), (7, 6, 5), (4, 3, 2)),
                            ((1, 2, 3), (4, 5, 6), (7, 8, 9)))))

# Weights for a layer: assuming a easy totally related layer
weights = torch.rand((3, 3, 3, 3))  # Random weights for demonstration

# Output after making use of weights (simplified)
output_data = torch.matmul(input_data, weights)

print(output_data.form)
# Output: torch.Dimension((2, 3, 3, 3))

Ở đây, input_data là một tenxơ bậc 4 biểu diễn một lô gồm hai hình ảnh RGB 3×3. Các trọng số cũng được biểu diễn dưới dạng một tenxơ, và dữ liệu đầu ra sau khi áp dụng các trọng số là một tenxơ khác.

Các phép toán Tensor

Các phép toán phổ biến trên tenxơ bao gồm:

• Các phép toán theo từng phần tử: Các phép toán được áp dụng độc lập cho từng phần tử, chẳng hạn như phép cộng và phép nhân.
• Phép nhân ma trận: Một trường hợp đặc biệt của sự co tenxơ trong đó hai ma trận được nhân để tạo ra ma trận thứ ba.
• Định hình lại: Thay đổi hình dạng của một tenxơ mà không làm thay đổi dữ liệu của nó.
• Chuyển vị: Hoán đổi kích thước của tenxơ.

Biểu diễn hình ảnh RGB 3×3 dưới dạng Tensor

Hãy xem xét một ví dụ thực tế trong học máy. Giả sử chúng ta có một hình ảnh được biểu diễn dưới dạng tenxơ 3 chiều có hình dạng (chiều cao, chiều rộng, kênh). Đối với hình ảnh màu, các kênh thường là Đỏ, Xanh lục và Xanh lam (RGB).

# Create a 3x3 RGB picture tensor
picture = np.array((((255, 0, 0), (0, 255, 0), (0, 0, 255)),
                  ((255, 255, 0), (0, 255, 255), (255, 0, 255)),
                  ((128, 128, 128), (64, 64, 64), (32, 32, 32))))

print(picture.form)

Ở đây, hình ảnh là một tenxơ có hình dạng (3, 3, 3) biểu diễn hình ảnh 3×3 với 3 kênh màu.

Triển khai CNN cơ bản để phân loại hình ảnh

Trong mạng nơ-ron tích chập (CNN) được sử dụng để phân loại hình ảnh, hình ảnh đầu vào được biểu diễn dưới dạng tenxơ và được truyền qua nhiều lớp, mỗi lớp biến đổi tenxơ bằng các phép toán như tích chập và gộp. Tenxơ đầu ra cuối cùng biểu diễn xác suất của các lớp khác nhau.

import torch
import torch.nn as nn
import torch.nn.practical as F  # Importing the practical module
# Outline a easy convolutional neural community
class SimpleCNN(nn.Module):
   def __init__(self):
       tremendous(SimpleCNN, self).__init__()
       self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3)
       self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
       self.fc1 = nn.Linear(16 * 3 * 3, 10)
   def ahead(self, x):
       x = self.pool(F.relu(self.conv1(x)))  # Utilizing F.relu from the practical module
       x = x.view(-1, 16 * 3 * 3)
       x = self.fc1(x)
       return x
# Create an occasion of the community
mannequin = SimpleCNN()
# Dummy enter knowledge (e.g., a batch of 1 grayscale picture of measurement 8x8)
input_data = torch.randn(1, 1, 8, 8)
# Ahead go
output = mannequin(input_data)
print(output.form)

Một loạt ảnh được biểu diễn bằng tenxơ bậc 4 input_data trong ví dụ này. Các tenxơ này được xử lý bởi các lớp tích chập và kết nối đầy đủ, áp dụng các phép toán khác nhau cho chúng để tạo ra kết quả mong muốn.

Phần kết luận

Tensor là các cấu trúc toán học mang ma trận, vectơ và vô hướng vào các chiều cao hơn. Chúng rất cần thiết cho vật lý lý thuyết và học máy, trong số các lĩnh vực khác. Các chuyên gia làm việc trong lĩnh vực học sâu và trí tuệ nhân tạo cần hiểu về tensor để sử dụng các khuôn khổ tính toán đương đại để thúc đẩy nghiên cứu, kỹ thuật và công nghệ.

Các câu hỏi thường gặp