[ad_1]
Trong Phần 1chúng ta đã thảo luận về cơ hội tấn công và phòng thủ tương đối trong Threat, trò chơi chinh phục thế giới. Vào cuối Phần 1, chúng ta đã kết luận rằng cuộc tấn công có 47,15% cơ hội giành chiến thắng trong trận chiến giành người lính đầu tiên và chúng ta tự hỏi làm thế nào những kẻ chinh phục nổi tiếng có thể đạt được chiến công của họ trong những điều kiện này. Chúng ta đã lưu phần thảo luận về người lính thứ hai cho Phần 2.
Để làm mới trí nhớ của chúng ta, trong Threat, bên tấn công tung được tối đa 3 viên xúc xắc, trong khi bên phòng thủ tung được tối đa 2 viên xúc xắc. Các lần tung cao nhất của mỗi bên được so sánh và bên thua sẽ mất một người lính, bên phòng thủ sẽ thắng trong trường hợp hòa. Tiếp theo, các lần tung cao thứ hai của mỗi bên được so sánh và một lần nữa, bên thua sẽ mất một người lính, bên phòng thủ sẽ thắng trong trường hợp hòa một lần nữa.
Vâng, chúng ta đã ở đây rồi. Hãy cùng tìm hiểu sâu hơn nhé.
(Đây vàBạn có thể tìm thấy mã trong đó tôi xác nhận các xác suất bên dưới.)
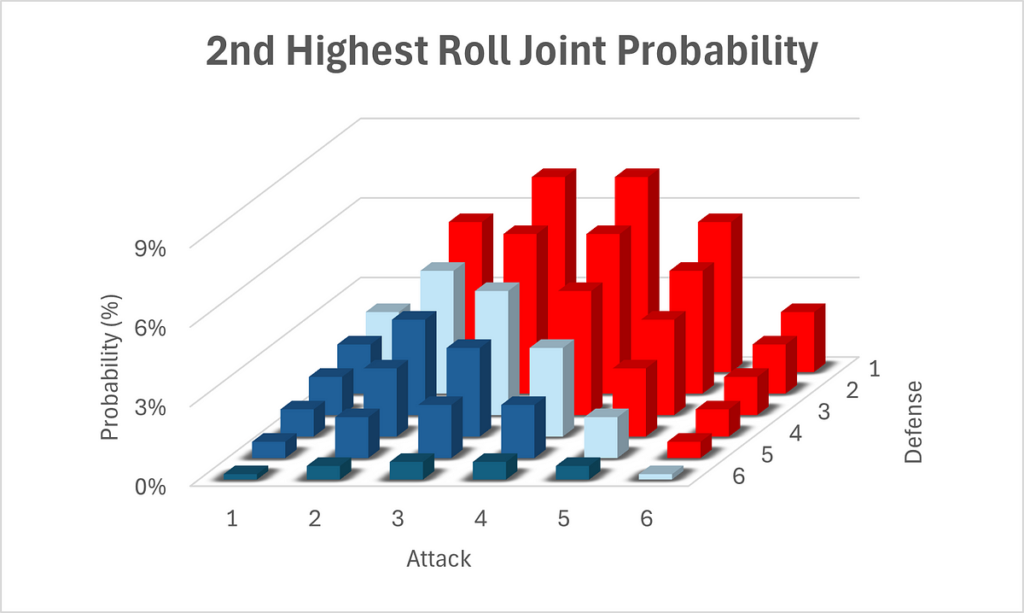
Tất nhiên, liên quan đến xác suất của người phòng thủ, chúng ta chỉ tính toán lần tung xúc xắc thấp nhất, vì anh ta chỉ có hai con xúc xắc. Do đó, xác suất là hình ảnh phản chiếu của xác suất mà chúng ta thấy liên quan đến lần tung xúc xắc cao nhất. Lần này, có 11 khả năng tạo ra lần tung xúc xắc cao thứ 2 là 1, 9 cho 2, 7 cho 3, v.v. Xác suất có thể được tính bằng cách chia cho 36, tổng số hoán vị có thể có cho hai con xúc xắc của bên phòng thủ.
Tính toán điểm cao thứ hai trong ba viên xúc xắc của người tấn công khác đáng kể so với phép tính của Phần 1. Tôi sẽ thành thật. Tôi đã vật lộn với điều này một chút. Trong các phép tính sau, hai điều phải được ghi nhớ.
- Chúng ta phải xem xét cả có bao nhiêu kết quả có thể xảy ra Và có bao nhiêu cách để mỗi kết quả có thể xảy ra. Ví dụ, kết quả của (6, 2, 3) tất nhiên là một kết quả duy nhất, nhưng nó có thể xảy ra theo 6 cách, tương ứng với mỗi giá trị xuất hiện trên xúc xắc nào. Nó có thể là bất kỳ {(2, 3, 6), (2, 6, 3), (3, 2, 6), (3, 6, 2), (6, 2, 3), (6, 3, 2)}. Do đó, kết quả này tương ứng với 1*6 = 6 hoán vị. Đối với một ví dụ khác, một kết quả với chính xác Hai đơn vị thực chất là tập hợp 5 kết quả, vì viên xúc xắc còn lại có thể có bất kỳ giá trị nào giữa 2 và 6. Và nó có thể xảy ra theo bất kỳ cách nào trong 3 cách sau, {(1, 1, x), (1, x, 1), (x, 1, 1)}, tương ứng với 3 vị trí có thể có của viên xúc xắc còn lại, vì vậy kết quả này thực sự tương ứng với 5*3 = 15 hoán vị.
- Chúng ta phải cẩn thận với các cặp đôi và bộ ba. Chúng phải được xem xét riêng biệt vì trong khi có 6 cách để có được kết quả là (1, 2, 3), chỉ có 3 cách để có được (1, 2, 2) và chỉ có 1 cách để có được (2, 2, 2).
Với những cân nhắc nêu trên, chúng tôi đã sẵn sàng tiến hành.
Hãy xem xét xác suất tung được số 1 cao thứ 2. Điều này khá dễ hiểu. Rõ ràng số thấp nhất cũng là 1. Bây giờ, chúng ta sẽ bỏ qua trường hợp cả 3 con xúc xắc đều là 1. Sau đó, con xúc xắc cao nhất có thể lấy bất kỳ giá trị nào giữa 2 và 6 và nó có thể xuất hiện trên bất kỳ con xúc xắc nào trong 3 con xúc xắc, vì chúng ta chưa chỉ rõ con xúc xắc nào trong 3 con xúc xắc có số cao nhất. Điều này tạo ra tổng cộng 3*5=15 hoán vị. Thêm trường hợp của bộ ba số 1 tạo ra tổng cộng 16 hoán vị. Theo một đối số đối xứng, chúng ta có thể tính toán rằng cùng một số hoán vị tạo ra số cao thứ 2 là 6.
Tiếp theo, thế còn việc có được 2 là lần tung cao thứ hai thì sao? Bây giờ, chúng ta sẽ bỏ qua khả năng có nhiều lần xuất hiện số 2 và giả sử lần tung cao nhất cao hơn 2 và lần tung thấp nhất thấp hơn 2. Lần tung cao nhất có thể có 4 giá trị (3–6) và lần tung thấp nhất phải là 1, tổng cộng có 4 kết quả và những kết quả này có thể xảy ra ở bất kỳ vị trí nào trong số 6 lần hoán vị của xúc xắc (3 khả năng cho vị trí của lần tung cao nhất (xúc xắc 1, xúc xắc 2 hoặc xúc xắc 3) và hai khả năng còn lại cho vị trí của lần tung thấp nhất), tổng cộng là 4*6=24 hoán vị. Bây giờ chúng ta sẽ xem xét hai lần xuất hiện số 2, nhưng không phải ba lần xuất hiện số 2. Nếu có chính xác 2 lần xuất hiện số 2, thì viên xúc xắc còn lại có thể có bất kỳ giá trị nào trong số 5 giá trị (trừ 2) và viên xúc xắc còn lại này có thể là bất kỳ viên xúc xắc nào trong số 3 viên xúc xắc, tổng cộng có 5*3=15 hoán vị. Thêm trường hợp cuối cùng của bộ ba 2, ta thu được tổng cộng 24+15+1 = 40 hoán vị. Một đối số track track cho kết quả tương tự cho lần tung thứ hai cao nhất là 5.
Cuối cùng, còn việc nhận được 3 hoặc 4 thì sao? Chúng ta hãy bắt đầu với 3. Một lần nữa bỏ qua khả năng có nhiều lần xuất hiện 3, lần tung cao nhất có thể lấy bất kỳ giá trị nào trong 3 giá trị (4, 5 hoặc 6) và lần tung thấp hơn có thể lấy bất kỳ giá trị nào trong 2 giá trị (1 hoặc 2), tổng cộng là 6 kết quả. Điều này một lần nữa có thể xảy ra ở bất kỳ 6 lần hoán vị nào của hai con xúc xắc, tổng cộng là 6*6 = 36 hoán vị. Trong trường hợp có chính xác 2 lần xuất hiện 3, con xúc xắc còn lại có thể lấy bất kỳ giá trị nào trong 5 giá trị (bất kỳ giá trị nào ngoài 3) và có thể xảy ra ở bất kỳ 3 con xúc xắc nào, tổng cộng là 5*3 = 15 hoán vị. Cộng khả năng cuối cùng của 3 lần xuất hiện 3 sẽ tạo ra tổng cộng 36+15+1=52 hoán vị. Một phép tính track track cũng tạo ra 52 hoán vị cho lần tung cao thứ hai là 4. Những kết quả này được tóm tắt trong hình ảnh bên dưới.
Lưu ý rằng xác suất kết quả tấn công là hoàn toàn đối xứng. Để chính xác về mặt toán học, P(x) = P(6-x). Chúng ta sẽ quay lại điểm này.
Tiếp theo chúng ta so sánh trực tiếp khả năng tấn công và phòng thủ.
Chúng ta có thể thấy rằng tấn công có lợi thế đáng kể ở đây. Nó có nhiều khả năng đạt được giá trị 4, 5 hoặc 6 hơn là phòng thủ.
[ad_2]
Source link